1.Evolution of sum

1.Evolution of sum
----------------

1.求整数和

def sum_integers(a, b):
    if a > b: return 0 # terminating point
    return a + sum_integers(a+1, b)
print(sum_integers(2, 4))

2.立方求和

def sum_cube(a, b):
    if a > b: return 0
    return cube(a) + sum_cube(a+1, b)

def cube(n):
    return pow(n, 3)

print(sum_cube(3, 5))

3.莱布尼茨求pi公式

def pi_sum(a, b):
    if a > b: return 0
    return 1 / (a * (a+2)) + pi_sum(a+4, b)
print(pi_sum(1, 10000)*8)
# 此处熟悉了if and return的写法, 这是if的最初形式.

2.Abstractions

2.Abstractions
------------

• 初步抽象

These three procedures clearly share a common underlying pattern. They are for the most part identical,

1. differing only in the name of the procedure,

2. the function of a used to compute the term to be added,

3. and the function that provides the next value of a.

We could generate each of the procedures by filling in slots in the same template:

(define (<name> a b)
  (if (> a b)
      0
      (+ (<term> a) ;;使用关键词term
         (<name> (<next> a) b)))) ;;next便是推导式样,
;;python的写法会隐藏很多的细节.

def name(a, b):
    if a > b: return 0
    return term(a) + name(next(a), b)

• 对比数学上的应用

The presence of such a common pattern is strong evidence that there is a useful abstraction waiting to be brought to the surface. Indeed, mathematicians long ago identified the abstraction of summation of a series and invented sigma notation,' for example:

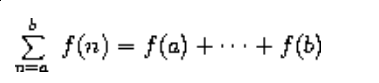
to express this concept. The power of sigma notation is that it allows mathematicians to deal with the concept of summation itself rather than only with particular sums – for example, to formulate general results about sums that are independent of the particular series being summed.

Similarly, as program designers, we would like our language to be powerful enough so that we can write a procedure that expresses the concept of summation itself rather than only procedures that compute particular sums. We can do so readily in our procedural language by taking the common template shown above and transforming the slots into formal parameters:

.. code:: commonlisp

   (defun sum(term a next b)
     (if (> a b)
         0
         (+ (term a)
            (sum term (next a) next b))))
   ;确实能够窥探其本质.
   ;這裏比python的sum好用.

def sum_recur(term, a, next, b):
    if a > b: return 0
    return term(a) + sum_recur(term, next(a), next, b)
# 找到思维上的漏洞．

3.Callbacks

Notice that sum takes as its arguments the lower and upper bounds a and b together with the procedures term and next. We can use sum just as we would any procedure. For example, we can use it (along with a procedure inc that increments its argument by 1) to define sum-cubes:

• sum_integers

def sum_integers(a, b):
    def identity(x): return x
    def inc(x): return x + 1
    return sum_recur(identity, a, inc, b)
print(sum_integers(1, 10))

print(sum(n for n in range(1, 10+1))) #identity

• sum_pi

def integral(f, a, b, dx):
    add_dx = lambda x: x + dx
    return sum_recur(f, a+(dx/2), add_dx, b) * dx

def cube(x): return x ** 3
print(integral(cube, 0, 1, 0.01))

4.Riemann Integral

4.Riemann Integral
----------------

def integral(f, a, b, dx):
    add_dx = lambda x: x + dx
    return sum_recur(f, a+(dx/2), add_dx, b) * dx


def sum_recur(term, a, next, b):
    if a > b: return 0
    return term(a) + sum_recur(term, next(a), next, b)

def cube(x): return x ** 3

print(integral(cube, 0, 1, 0.01))

与iteration对比

def integral(f, a, b, dx):
    return sum(f(a+(dx/2)+n*dx) for n in range(int((b-a)/dx)) ) * dx

print(integral(cube, 0, 1, 0.00000001))